1.2 Example 2: a simple stack example

The next example shows how to calculate the scattering matrix of a stack of waveguides and how to loop over a simulation parameter:

#!/usr/bin/env python

####################################################################
#
# Simple stack example
#
####################################################################

from camfr import *

set_lambda(1)
set_N(20)
set_polarisation(TE)

# Define materials.

GaAs = Material(3.5)
air  = Material(1.0)

# Define slabs.

slab  = Slab(air(2) + GaAs(0.5) + air(2))
space = Slab(air(4.5))

# Print the reflectivity for different lengths.

for L in arange(0.005, 0.100, 0.005):
    stack = Stack(space(0) + slab(L) + space(0))
    stack.calc()
    print L, abs(stack.R12(0,0))

Apart from the same slab waveguide as in the previous example, we also define a second slab called space, a uniform air layer.

Let us skip ahead to this line:

    stack = Stack(space(0) + slab(L) + space(0))

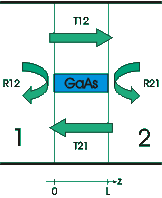
This line defines a stack consisting of a sequence of waveguide sections, as shown in fig. 2:

Because of the way eigenmode expansion works, the incidence and exit waveguides (space in this case) are infinitely long. The thickness of the sections space(0) just serve to indicate the location of the reference input and output planes.

The command stack.calc() is used to calculate the scattering matrix of the stack named stack. Fig. 2 indicates the meaning of the four submatrices of this scattering matrix. There are two reflection and transmission matrices, for incidence from either medium 1 or medium 2.

More specifically, if you have e.g. an incident field from the left in medium 1 , described by a column vector f of expansion coefficients, the reflected field will be described by the product R12 x f.

So, stack.R12(0,0) is the reflection coefficient of the fundamental mode of the incident waveguide back to itself.

Also illustrated in this example is how to create loops in Python, e.g. to vary the length in central waveguide section from 5 to 100 nm (excluding 100 nm) in steps of 5 nm:

for L in arange(0.005, 0.100, 0.005):
    stack = Stack(space(0) + slab(L) + space(0))
    stack.calc()
    print L, abs(stack.R12(0,0))

The function arange is not part of the core Python language, but rather of the extension package NumPy.

Very important to notice is that Python uses indentation to distinguish statements which form part of the loop and which don't. So, writing

for L in arange(0.005, 0.100, 0.005):
    stack = Stack(space(0) + slab(L) + space(0))
    stack.calc()
print L, abs(stack.R12(0,0))

would only print out the results for the last value of L, which incidentally is 0.095. It does not really matter if you use tabs or spaces to indent, as long as you are consistent.

It is of course trivial to create nested loops:

for x in arange(0.000, 0.100, 0.010):
    for y in arange(0.000, 0.200, 0.020):
        do_something()

This document was generated by root on August, 27 2008 using texi2html 1.76.